Reflectance and Color Selection - Concepts

The Reflectance and Color Selector dialog is used to choose Color, and its associated reflectance, for all reflective surface specification in AGi32. The dialog is composed of graphic color selection as well as manual HSL and RGB specification for selecting an exact color choice.

Graphic Color Selection

AGi32 provides a graphic HSL selection method for an intuitive approach. The HSL method matches human perception of color by first prompting for a color (hue), then a shade of that hue (Saturation and Luminance).

Each of the three components (Hue, Saturation and Luminance) are measured on a scale from 0 to 240. Hue provides the absolute color choices such as green and blue. The hues are arranged in a linear strip from Red at the top (240), through the Color Spectrum - Violet (200), Indigo (170), Blue (128), Green (85), Yellow (42), Orange (21) - then back to Red (0).

Saturation indicates the pureness, or intensity, of a hue, or the amount of gray it contains. A vivid color typically has a high saturation level (low gray selection). As the saturation decreases, the amount of gray increases, and the color becomes less vivid. Saturation is sometimes called Chroma.

Luminance indicates the lightness of the color. A luminance value of 0 indicates the final color is black. A value of 240 produces a pure white color. Pure black and white colors do not exist in the architectural surface realm, so more realistic (and typically muted colors) should be used for accurate lighting simulations. This characteristic is sometimes called Value.

Color and Reflectance

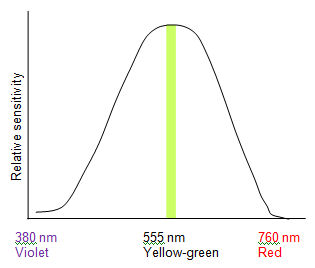
The human eye is visually sensitive to a small portion of the electromagnetic spectrum between 400 and 700 nanometers. We are not equally sensitive to all wavelengths (colors). The variation in sensitivity is described by the CIE Photopic spectral luminous efficiency function and is shown graphically with a bell curve. The shape of the curve indicates that our eyes are most sensitive to yellow-green, and exhibit lesser sensitivity to violet and red (our eyes respond least to violet light).

 

Computer monitors display all colors as a mix of the three primary additive colors: Red, Blue and Green. Much of the visible spectrum that humans perceive can be duplicated by this color space, but not all colors (especially saturated colors) can be simulated.

The relationship between grayscale reflectance (overall reflectance) of a surface and its RGB color equivalent is as follows:

Grayscale Reflectance  = 0.2125 * R + 0.7154 * G + 0.0721 * B.

From this relationship we can derive the following assumptions:

• The maximum reflectance a saturated Red color can exhibit is 21%.
• The maximum reflectance a saturated Blue color can exhibit is 7%.
• The maximum reflectance a saturated Green color can exhibit is 72%.
• Surfaces with high reflectances always have a large green component in their color makeup.

Transmittance relationship to reflectance value

Transmittance is mathematically related to the color of the surface. AGi32 automatically computes the maximum non-dichroic transmittance possible for surfaces where applicable and displays this value in the transmittance cell. The relationship is based on the premise that all light that is not reflected or absorbed can be transmitted.

Transmittance Equation:

Transmittance = (0.2125)(Ravail) + (0.7154)(Gavail) + (0.0721)(Bavail)

To compute the maximum transmittance for any particular color we first must find the percentage of each component (Red, Green, Blue) that is available for transmittance.

Example:

Suppose we have a color (somewhat of a subdued red) with the following components, R=210, G=105, B=105. What is the maximum transmittance?

Begin by computing the percentages of each component that can be reflected. What is not reflected or absorbed is then available to be transmitted. We know that full saturation of any color is 255. Divide each component by 255 to find the maximum amount that can be reflected.

• Max reflected R = 210/255 = 0.824
• Max reflected G = 105/255 = 0.412
• Max reflected B = 105/255 = 0.412

To find the maximum amount of light that can be transmitted we must look at which component of the color allows the most light to be reflected, as this color then has the least amount of available light remaining to transmit. In non-dichroic transmittance, the other colors must follow in proportion. In our example, the Red (R) component has the greatest reflected component (that's why it looks red). The maximum transmitted amount of red is then whatever is remaining after reflection.

• Max transmitted R = 1 - 0.824 = 0.176
• The ratio of transmitted to reflected light for red is 0.176/0.824 = 0.2135
• Apply this multiplier to the other color components to arrive at the relative amounts of light that can be transmitted:
• Green: 0.2135 x 0.412 = 0.088
• Blue: 0.2135 x 0.412 = 0.088

Note that Red also has the greatest transmitted component, so the light that passes through will be reddish in appearance.

Now plug these relative amounts of transmissible light into the equation for Transmittance.

Transmittance = (0.2125)(0.176) + (0.7154)(0.088) + (0.0721)(0.088) = 0.1004

The maximum transmittance for our example color is then 0.1004, or roughly ten percent. (As a side note, since 50% of the light striking this surface was reflected and 10% was transmitted, that leaves 40% to be absorbed.)